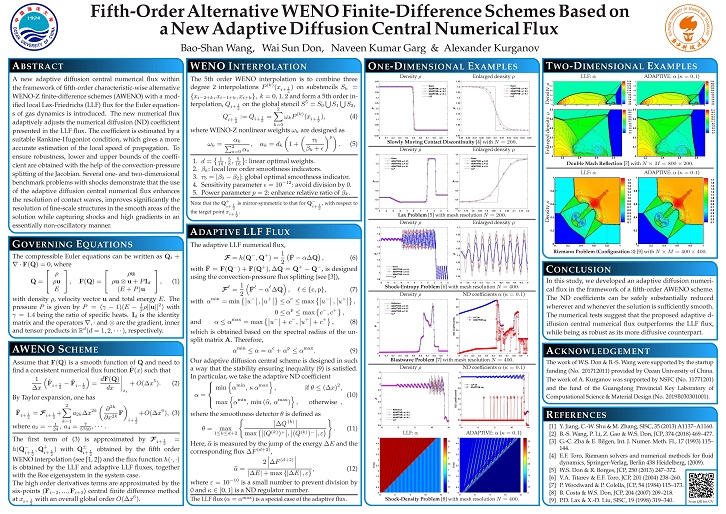
The new numerical flux adaptively adjusts the numerical diffusion coefficient presented in the LLF flux. The coefficient is estimated by a suitable Rankine-Hugoniot condition, which gives a more accurate estimation of the local speed of propagation. To ensure robustness, lower and upper bounds of the coefficient are obtained with the help of the convection-pressure splitting of the Jacobian.

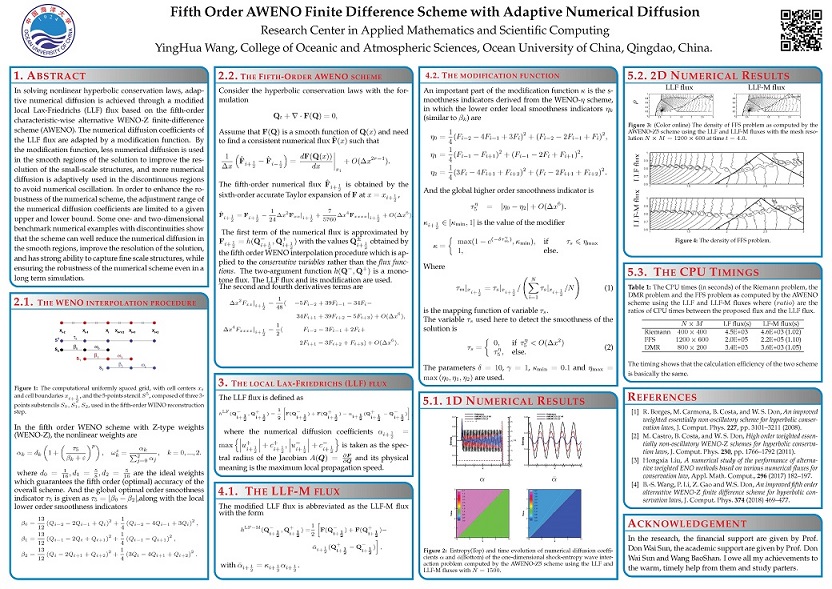
The numerical diffusion coefficients of the LLF flux are adapted by a modification function. By the modification function, less numerical diffusion is used in the smooth regions of the solution to improve the resolution of the small-scale structures, and more numerical diffusion is adaptively used in the discontinuous regions to avoid numerical oscillation.

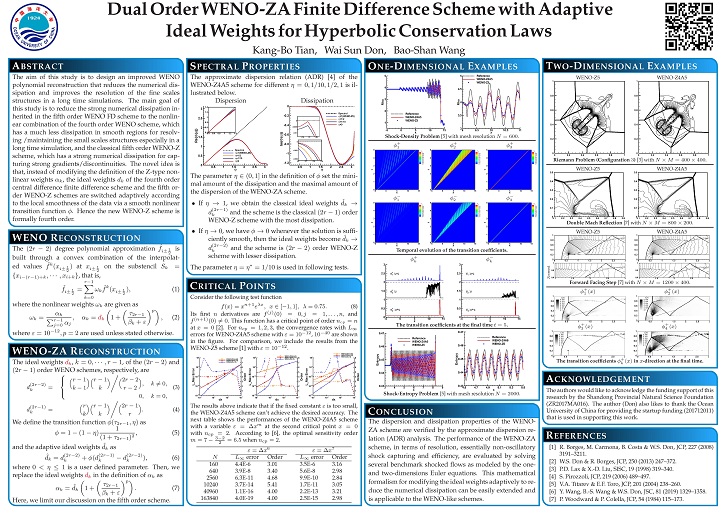
A simple yet efficient dual order WENO-ZA finite difference scheme with an adaptive ideal weights is designed. It is adaptively controlled by a modifier function along with a user defined parameter between zero and one that control the least amount of dissipation to be added to the fourth order scheme.

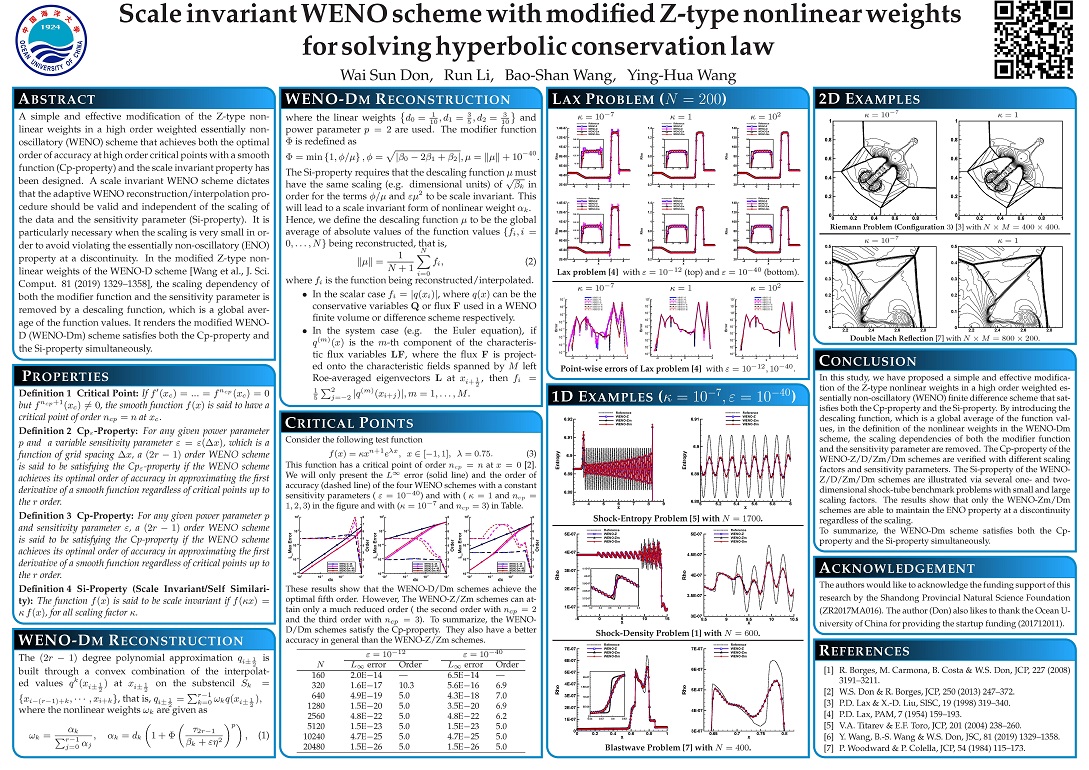
A simple and effective modification of the Z-type nonlinear weights in a high order weighted essentially nonoscillatory (WENO) scheme that achieves both the optimal order of accuracy at high order critical points with a smooth function (Cp-property) and the scale invariant property has been designed.