Overestimated Quasi-conservative Formulation (2018.11.28)
The overestimated quasi-conservative form is implemented to simulate compressible multicomponent flow fields. The WENO scheme is written in the split form that has the consistent and dissipation parts of the numerical flux.
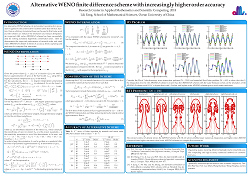
AWENO scheme (2018.11.26)
An improved fifth order AWENO-Z scheme has been successfully used for solving nonlinear hyperbolic conservation laws. Here we demonstrate the improved performance of seventh order and ninth order AWENO-Z schemes.
WENO Scheme (2018.11.26)
A fifth order WENO scheme is used to numerically approximate the solution of Euler equation. The performance will be better if the fluxes are projected on the characteristic fields before WENO reconstruction procedure is carried out.
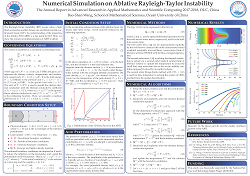
Numerical Simulation on ARTI (2018.11.28)
An understanding of the properties of the ARTI, where a low density and high pressure ablating plasma accelerates the high density shell, is a key point for ICF. Here, we show the numerical implementations of ARTI in detail.
Non-oscillatory Central Differencing (2018.11.28)
Many of the developed high-resolution schemes are based on upwind differencing. The building block of these schemes is the
averaging of an approximate Godunov solver. Its time consuming part involves the field-by-field decomposition which is required in order to identify the "direction of the wind".