AWENO-Z scheme for compressible multicomponent flows (2019.7.31)
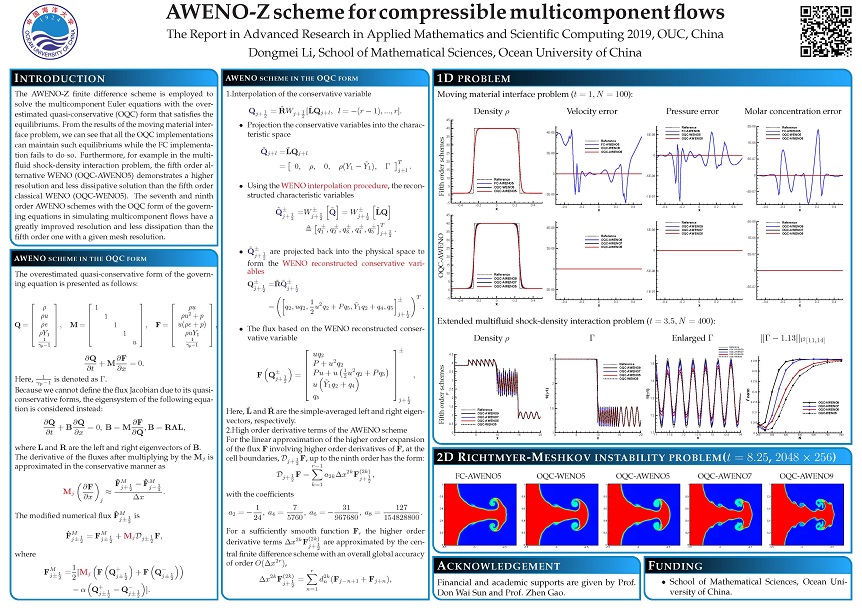
The AWENO-Z finite difference scheme is employed to solve the multicomponent Euler equations with the overestimated quasi-conservative form that satisfies the equilibriums.
Well-Balanced AWENO Scheme for Euler Equations under Gravitational Fields (2019.7.31)
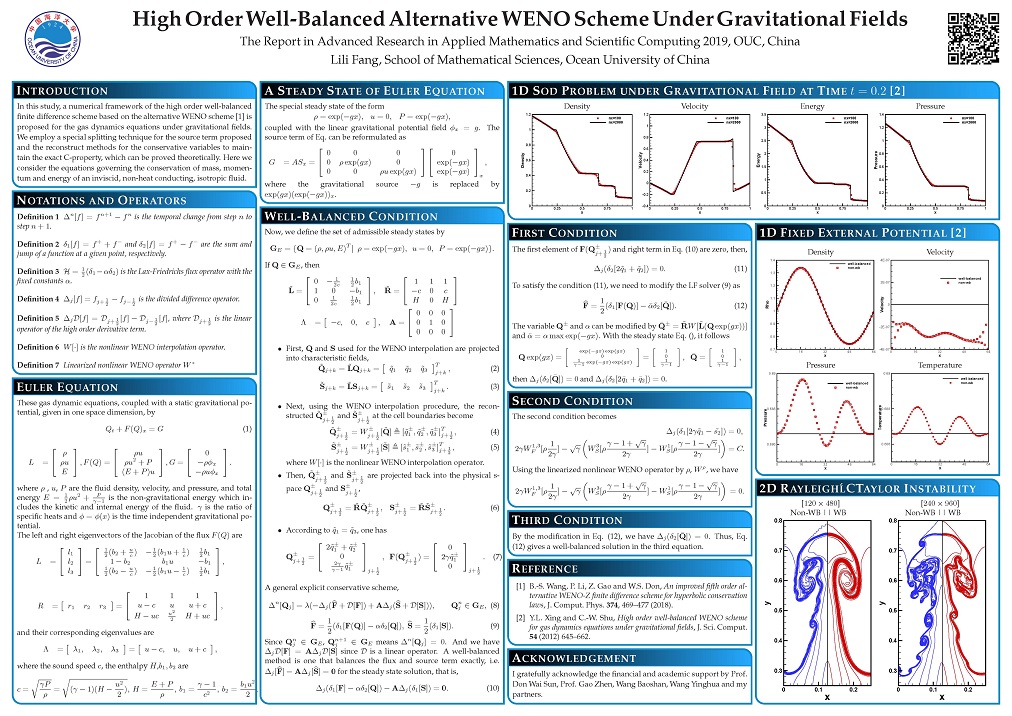
In this study, a numerical framework of the high order well-balanced finite difference scheme based on the alternative WENO scheme is proposed for the gas dynamics equations under gravitational fields with a special splitting technique for the source term and the conservative variables to maintain the exact C-property.
Well-Balanced Generalized WENO-Interpolation Schemes for Shallow Water Equations (2019.7.31)
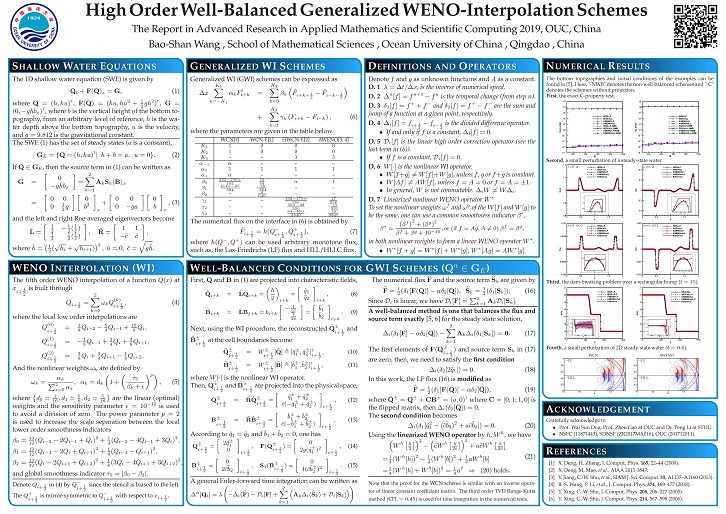
In this work, the well-balanced generalized WENO-interpolation schemes are applied to the shallow water equations. Several linear and nonlinear numerical operators such as the linearized nonlinear WENO operator and their mathematical properties are defined to build the general conditions to maintain the exact C-property.
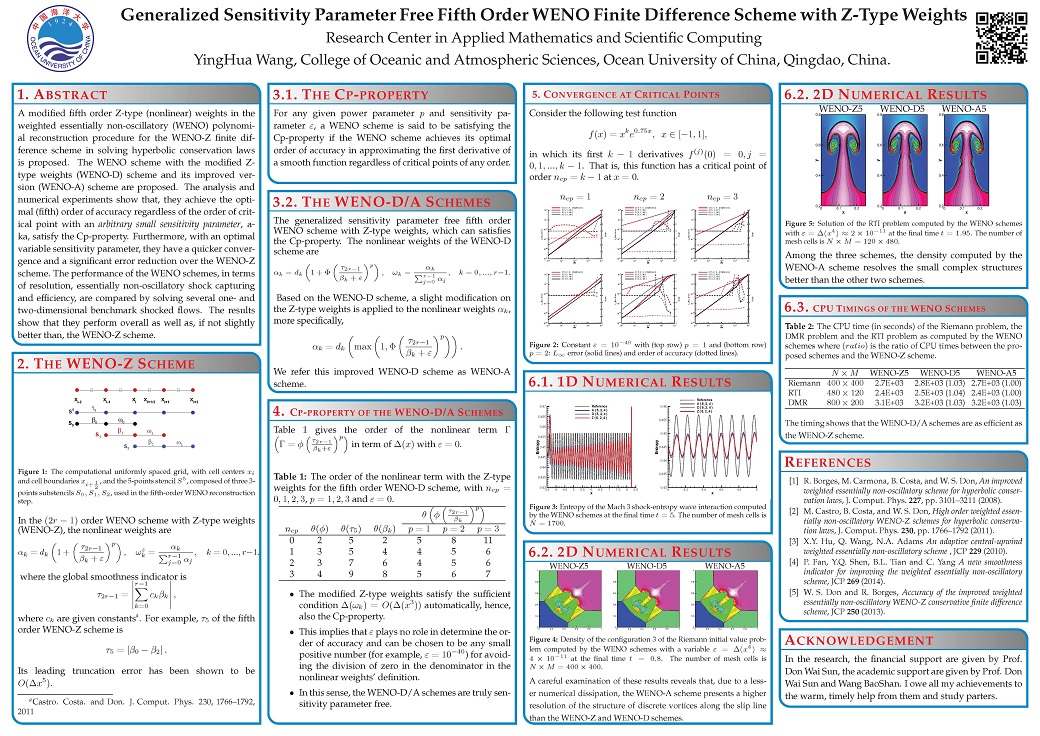
Forth Order Central-Upwind WENO Scheme with Modified Ideal Weights (2019.7.31)
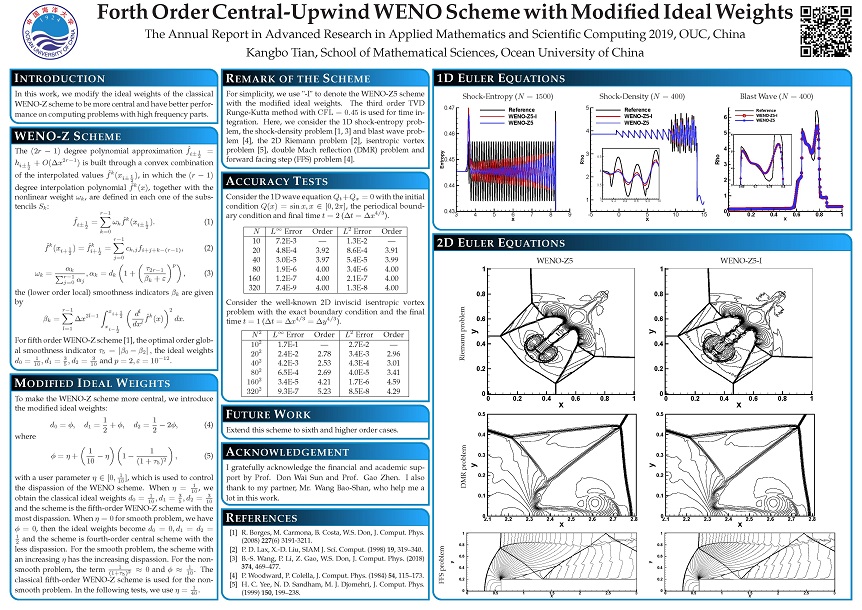
In this work, we modify the ideal weights of the classical WENO-Z scheme to be more central and have better performance on computing problems with high frequency parts.
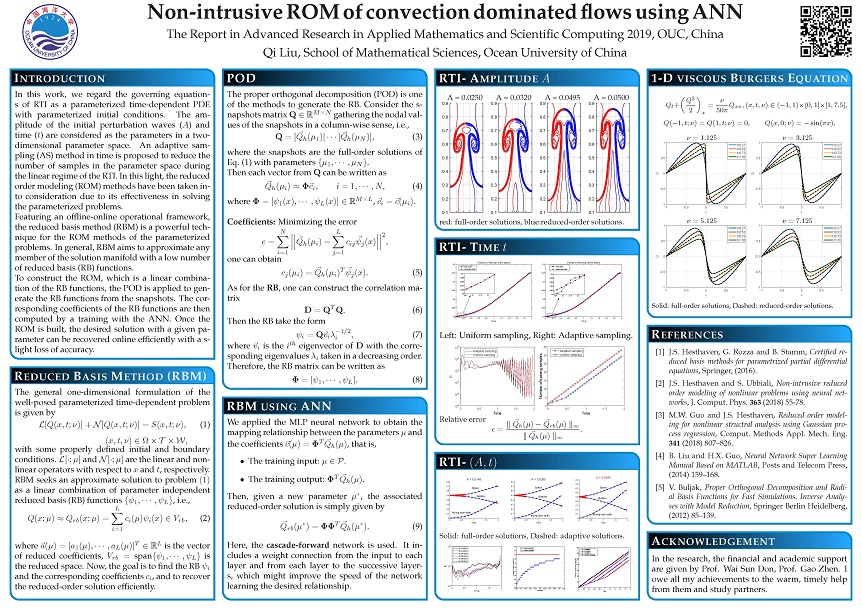
Non-intrusive ROM of convection dominated flows using ANN (2019.7.31)
In this work, the POD is applied to generate the RB functions from the snapshots. The corresponding coefficients of the RB functions are then computed by a training with the ANN. Once the ROM is built, the desired solution with a given parameter can be recovered online efficiently with a slight loss of accuracy.
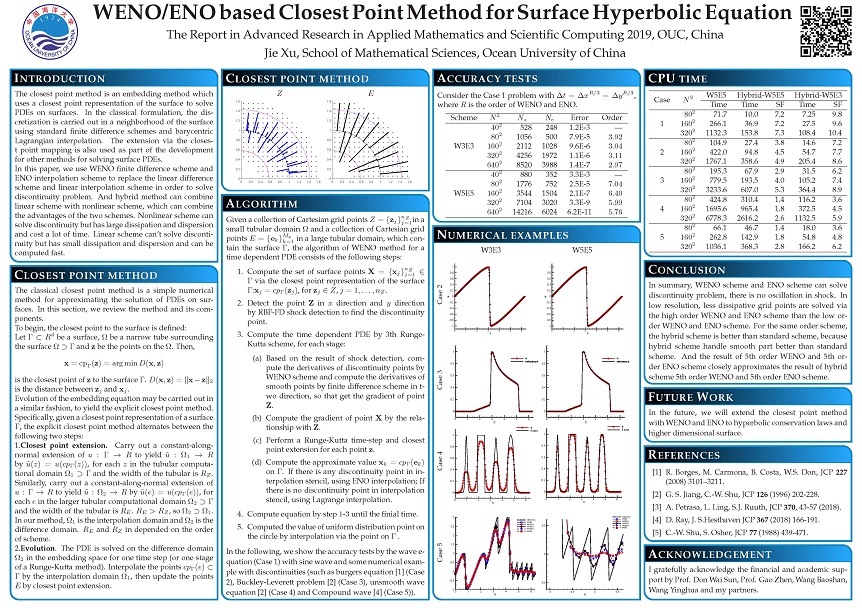
WENO/ENO based Closest Point Method for Surface Hyperbolic Equation (2019.7.31)
The closest point method is an embedding method which uses a closest point representation of the surface to solve PDEs on surfaces. In this paper, we use WENO and ENO based closest point method (and hybrid method) to replace the linear difference scheme and linear interpolation scheme in order to solve discontinuity problem on the surface.
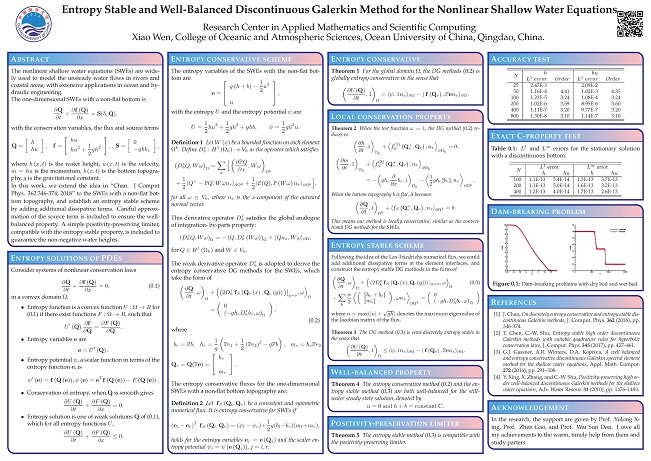
Entropy Stable and Well-Balanced DG methods (2019.8.19)
In this work, we extend the idea in “Chan. J Comput Phys. 362:346-374, 2018” to the shallow water equations with a non-flat bottom topography, and establish an entropy stable scheme by adding additional dissipative terms.
New modified fifth order WENO-Z scheme. (2019.8.19)
We design a new modified fifth order WENO-Z scheme. We will give proof of our theory and numerically results on smooth function in the presence of critical points to confirm our theory.