Well-Balanced DG Method
The well-balanced discontinuous Galerkin methods for the shallow water equations can almost maintain the still water steady state exactly, and at the same time can almost preserve the nonnegativity of the water height without loss of mass conservation.
Fourier Collocation Method
We present a high order numerical scheme for two-dimensional incompressible Navier-Stokes equations based on the vorticity streamfunction formulation with periodic boundary conditions.
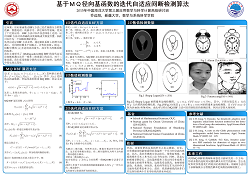
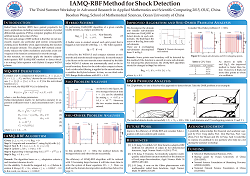
IAMQ-RBF Method
In this research, we apply the iterative adaptive multiquadric RBF (IAMQ-RBF) method to detect the shocks in Hybrid Compact-WENO scheme for solving Euler equations.
IAMQ-RBF Method
In this research, we use IAMQ-RBF method for detection of discontinuities in 1D and 2D problems. For the two-dimensional problems, we use a slice-by-slice approach.
MPI Parallel Computing
We discussed a new MPI algorithm so that the MPI program could reduce communication wait time and get the accurate results.
WENO-Z Scheme
The main objective of this work is to study the 5th order WENO finite difference scheme which is capable of capturing sharp discontinuities in an essentially nonoscillatory manner.
Well-Balanced Hybrid Scheme
In this work, we investigate the performance of the high order well-balanced Hybrid Compact-WENO scheme for simulations of shallow water equations with source terms due to a non-flat bottom topography.
Compact FD Scheme
We mainly show four compact FD schemes (CFDSs), including centered compact scheme, centered compact scheme with spectral-like resolution and two CFDSs for non-uniform grid.